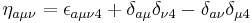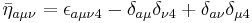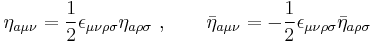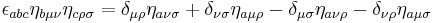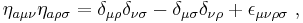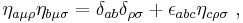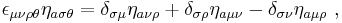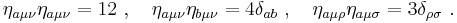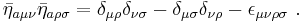't Hooft symbol

The 't Hooft η symbol is a symbol which allows one to express the generators of the SU(2) Lie algebra in terms of the generators of Lorentz algebra. The symbol is a blend between the Kronecker delta and the Levi-Civita symbol. It was introduced by Gerard 't Hooft. It is used in the construction of the BPST instanton. They are defined by

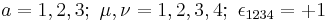( $a=1,2,3�;~ \mu,\nu=1,2,3,4�;~ \epsilon_{1 2 3 4}=%2B1$ )

$\eta_{a \mu \nu} = \epsilon_{a \mu \nu 4} %2B \delta_{a \mu} \delta_{\nu 4} - \delta_{a \nu} \delta_{\mu 4}$

$\bar \eta_{a \mu \nu} = \epsilon_{a \mu \nu 4} - \delta_{a \mu} \delta_{\nu 4} %2B \delta_{a \nu} \delta_{\mu 4}$

The (anti)self-duality properties are

$\eta_{a\mu\nu} = \frac{1}{2} \epsilon_{\mu\nu\rho\sigma} \eta_{a\rho\sigma} \ , \qquad \bar\eta_{a\mu\nu} = - \frac{1}{2} \epsilon_{\mu\nu\rho\sigma} \bar\eta_{a\rho\sigma} \$

Some other properties are

$\epsilon_{abc} \eta_{b\mu\nu} \eta_{c\rho\sigma} = \delta_{\mu\rho} \eta_{a\nu\sigma} %2B \delta_{\nu\sigma} \eta_{a\mu\rho} - \delta_{\mu\sigma} \eta_{a\nu\rho} - \delta_{\nu\rho} \eta_{a\mu\sigma}$

$\eta_{a\mu\nu} \eta_{a\rho\sigma} = \delta_{\mu\rho} \delta_{\nu\sigma} - \delta_{\mu\sigma} \delta_{\nu\rho} %2B \epsilon_{\mu\nu\rho\sigma} \ ,$

$\eta_{a\mu\rho} \eta_{b\mu\sigma} = \delta_{ab} \delta_{\rho\sigma} %2B \epsilon_{abc} \eta_{c\rho\sigma} \ ,$

$\epsilon_{\mu\nu\rho\theta} \eta_{a\sigma\theta} = \delta_{\sigma\mu} \eta_{a\nu\rho} %2B \delta_{\sigma\rho} \eta_{a\mu\nu} - \delta_{\sigma\nu} \eta_{a\mu\rho} \ ,$

$\eta_{a\mu\nu} \eta_{a\mu\nu} = 12 \ ,\quad \eta_{a\mu\nu} \eta_{b\mu\nu} = 4 \delta_{ab} \ ,\quad \eta_{a\mu\rho} \eta_{a\mu\sigma} = 3 \delta_{\rho\sigma} \ .$

The same holds for 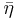$\bar\eta$ except for

$\bar\eta_{a\mu\nu} \bar\eta_{a\rho\sigma} = \delta_{\mu\rho} \delta_{\nu\sigma} - \delta_{\mu\sigma} \delta_{\nu\rho} - \epsilon_{\mu\nu\rho\sigma} \ .$

Obviously 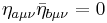$\eta_{a\mu\nu} \bar\eta_{b\mu\nu} = 0$ due to different duality properties.

Many properties of these are tabulated in the appendix of 't Hooft's paper^[1] and also in the article by Belitsky et al.^[2]

't Hooft symbol

See also

References